( ZF Bortz, S. 187 -191 ) Bei der Überprüfung von Zusammenhangshypothesen interessieren uns die Zusammenhänge , die zwischen verschiedenen Merkmalen bestehen. Dabei unterscheiden wir zwischen positiven Zusammenhängen d.h., in beiden Merkmalen ist eine hohe bzw niedrige Ausprägung zu beobachten und negativen Zusammenhängen d.h. , während in einem Merkmal eine hohe Ausprägung zu beobachten ist, stellen wir im anderen eine niedrige fest und umgekehrt.
Wiederholung Varianz :
Erweiterung der Varianzformel auf zwei unterschiedliche Variablen ; die Kovarianz :
Die Kovarianz gibt das Ausmaß des linearen Zusammenhangs zwischen zwei Variablen wieder. Je größer der Betrag der Kovarianz, umso größer ist der lineare Zusammenhang ( positiv oder negativ). Sind zwei Variablen unabhängig, so haben sie eine cov von 0.
Um eine Standardartisierung der Kovarianz zu erreichen wird sie am Produkt der Streuungen der eingehenden Variablen relativiert. Wir erhalten somit den Korrelationskoeffizienten r .
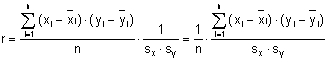
Kovarianz und Korrelation stehen in einer definierten Relation
Die Korrelation zweier Variablen entspricht dem Produkt Ihrer z-Werte geteilt durch n:
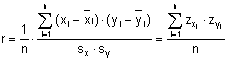
Der Korrelationskoefizient ist durch seine Relativierung an den Streuungen gegenüber Veränder-ungen der Einheit bzw. des Maßstabs der Variablen invariant.
Wertebereich des Korrelationskoeffizienten :
r=-1 perfekt negativer Zusammenhang
r= 0 kein linearer Zusammenhang
r= 1 perfekt positiver Zusammenhang ( die beiden Variablen sind identisch )


